Parallelograms in the coordinate plane
Construct a figure like this one with Sketchpad using the following steps.
In the graph menu,
- Choose Define New Parameter, and make the parameter 1 cm. Don't forget the unit!
- With the parameter selected on the screen, choose Define Unit Distance.
- Also, check the item Snap Points.
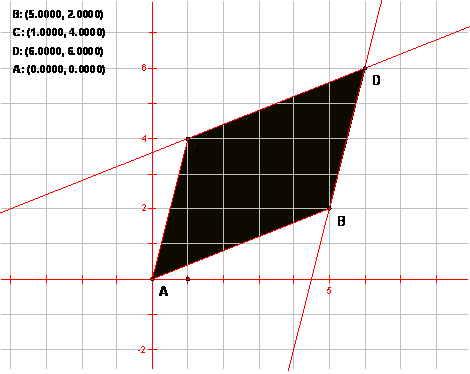
Then, letting A be the origin, draw segments AB and AC. Construct a parallelogram ABDC.
- Select all 4 points and choose Measure > Coordinates. If the points have snapped properly, then the coordinates should all be integers.
- Write down the coordinates of the points A, B, C, D.
- Also, measure the equation of line CD.
Now let E be the intersection of the y-axis and the line CD (i.e., the y-intercept). Construct point F so that ABFE is a parallelogram.
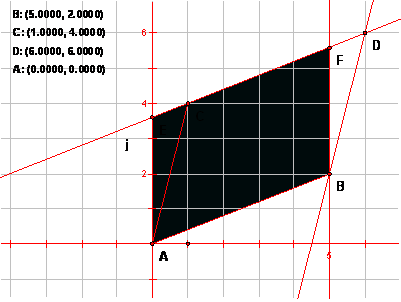
- Measure the areas of ABDC and ABFE. How do they compare. Why?
- Using the segment AE as the base, what are the measures of the base and height of ABFE?
Getting a Formula
Now follow this same construction process but this time instead of numbers, use letters for the coordinates. Let B = (a,b) and C = (c, d).
- Find the equation of line CD and the coordinates of E.
- Then compute the base and height of ABFE and find the area.
- Then tell how this area compares with the original area of ABDC.
You should have a formula for the area of the parallelogram
ABDC without doing a gruesome calculation involving the height of ABDC because
you found the area of a simpler parallelogram with the same area.
You may find the expression in the formula looks familiar from another
course.